Drawing Awesome Spiral Shapes using Python Turtle Module
Contents
Introduction
The Logo programming language is frequently linked to turtle graphics. In the late 1960s, Seymour Papert added turtle graphics support to Logo to support his version of the turtle robot, which is a simple robot controlled from the user’s workstation and designed to carry out the drawing functions assigned to it using a small retractable pen set into or attached to the robot’s body.
The standard library of the Python programming language now contains a Turtle graphics module. Turtle in Python, like its Logo ancestor, allows programmers to manipulate one or more turtles in a two-dimensional space.
Overview of the syntax
A location, an orientation (or direction), and a pen are the three qualities of the turtle. Color, width, and on/off state are all properties of the pen (also called down and up).
“Move ahead 10 spaces” and “turn left 90 degrees” are orders that the turtle responds to based on its current location. The turtle’s pen can also be managed by enabling it, changing its color, and adjusting its breadth. By visualizing what they would do if they were the turtle, a pupil may comprehend (and forecast and reason about) the turtle’s motion. This is referred to as “body syntonic” reasoning by Seymour Papert.
Basic syntax:
import turtle // start of the program
//body
//of the main
//code
turtle.done() //end of the programInorder to understand the codes to draw various shapes given below, Getting Started with Powerful yet Easy Python Graphics Module, Turtle.
Methods
A Python method is a label that can be applied to an object and is a piece of code that may be run on that object.
The most frequently, used turtle methods are:
| Method | Parameter | Description |
|---|---|---|
| Turtle() | None | Creates and returns a new turtle object |
| forward() | amount | Moves the turtle forward by the specified amount |
| backward() | amount | Moves the turtle backward by the specified amount |
| right() | angle | Turns the turtle clockwise |
| left() | angle | Turns the turtle counterclockwise |
| penup() | None | Picks up the turtle’s Pen |
| pendown() | None | Puts down the turtle’s Pen |
| up() | None | Picks up the turtle’s Pen |
| down() | None | Puts down the turtle’s Pen |
| color() | Color name | Changes the color of the turtle’s pen |
| fillcolor() | Color name | Changes the color of the turtle will use to fill a polygon |
| heading() | None | Returns the current heading |
| position() | None | Returns the current position |
| goto() | x, y | Move the turtle to position x,y |
| begin_fill() | None | Remember the starting point for a filled polygon |
| end_fill() | None | Close the polygon and fill with the current fill color |
| dot() | None | Leave the dot at the current position |
| stamp() | None | Leaves an impression of a turtle shape at the current location |
| shape() | shapename | Should be ‘arrow’, ‘classic’, ‘turtle’ or ‘circle’ |
Drawing Spiral Shape
Drawing Spiral Shape using python turtle module is like learning anything else really. You learn the basic concept and then you can do the same with any other shape. Let me explain!!
In each cycle, the length of the side is reduced by a set number, resulting in spiral figures. Given below are the steps through which you can make a spiral out of any shape.
- Choose a figure’s side length and assign it to a variable side. The side of a figure, for example, is 20 units.
side = 20- Run a for loop for a long time, and use the forward() and right() functions of the turtle module in that loop. The side variable should be passed to the forward() function, and the value of a figure’s exterior angle should be passed to the right() function. After that, reduce the side’s length by a certain amount.
for i in range(20):
t.forward(side)
t.right(exteriorAngle)
side = side - 2Spiral Square
For obtaining a spiral square,
- Import turtle.
- Set tom as our turtle object.
- Set the speed to 2.
- Set side as 200.
- Run a loop like mentioned above.
- turtle.done().
import turtle
tom = turtle.Turtle()
tom.speed(2)
side = 200
for i in range(100):
tom.forward(side)
tom.right(90) #Exterior angle of a square is 90 degree
side = side - 2
turtle.done()Output
The output for the spiral square is as follows. You can see, multiple squares overlapping over each other to form a Spiral Square.

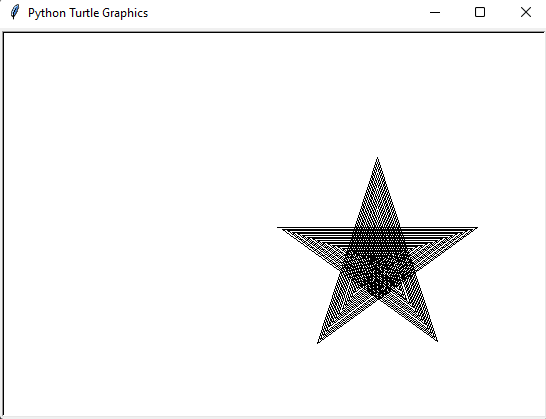
Spiral Star
For obtaining a spiral star,
- Import turtle.
- Set tom as our turtle object.
- Set the speed to 2.
- Set side as 2.
- Run a loop like mentioned above.
- turtle.done().
import turtle
tom = turtle.Turtle()
tom.speed(200)
side = 2
for i in range(100):
tom.forward(side)
tom.right(144) #Exterior angle of a star 144 is degree
side = side - 2
turtle.done()Output
The output for the spiral star is as follows. You can see, multiple stars overlapping over each other to form a Spiral Star.
Spiral Triangle
For obtaining a spiral triangle,
- Import turtle.
- Set tom as our turtle object.
- Set the speed to 2.
- Set side as 2.
- Run a loop like mentioned above.
- turtle.done().
import turtle
tom = turtle.Turtle()
tom.speed(2)
side = 2
for i in range(70):
tom.forward(side)
tom.right(120) #Exterior angle of a triangle 120 is degree
side = side - 3
turtle.done()Output
The output for the spiral triangle is as follows. You can see, multiple triangles overlapping over each other to form a Spiral Triangle.

Spiral Pentagon
For obtaining a spiral pentagon,
- Import turtle.
- Set tom as our turtle object.
- Set the speed to 2.
- Set side as 2.
- Run a loop like mentioned above.
- turtle.done().
import turtle
tom = turtle.Turtle()
tom.speed(2)
side = 2
for i in range(104):
tom.forward(side)
tom.right(72) #Exterior angle of a pentagon 72 is degree
side = side - 2
turtle.done()Output
The output for the spiral pentagon is as follows. You can see, multiple pentagons overlapping over each other to form a Spiral Pentagon.

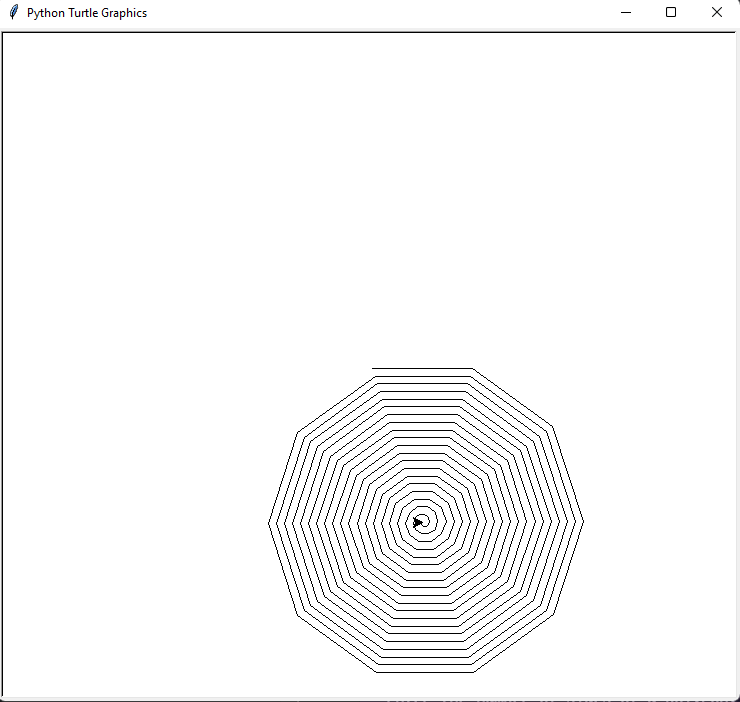
Spiral Polygon
Any two-dimensional geometry made up of straight lines is called a polygon. Polygons include triangles, quadrilaterals, pentagons, and hexagons, among others. The name of the shape indicates how many sides it has. A triangle, for example, has three sides, while a quadrilateral has four.
For obtaining a spiral star,
- Import turtle.
- Set tom as our turtle object.
- Set the speed to 2.
- Set side as a user input variable.
- Set length as a user input variable.
- Calculate the exterior angle as 360/side.
- Run a loop like mentioned above.
- turtle.done().
import turtle
tom = turtle.Turtle()
tom.speed(2)
side = int(input('Enter the number of sides of a polygon: '))
length = int(input('Enter the length of a side of a polygon: '))
exteriorAngle = 360/side
for i in range(200):
tom.forward(length)
tom.right(exteriorAngle)
length = length - 0.5
turtle.done()Output
The output for the spiral polygon is as follows. You can see, multiple polygons overlapping over each other to form a Spiral Polygon. As multiple shapes are polygons, the user can define the sides and length of each side of the polygon. For this instance we take 10 sides each of length 100.

The output is as follows for the above input: