Matrix Multiplication in C

Introduction

The C programming language is a procedural programming language. Between 1969 and 1973, Dennis Ritchie worked on the project. It was created primarily as a system programming language for developing operating systems.

In order to understand the code given below you’ve got to have prior knowledge and or understanding of the following topics:

• C for Loop
• C Arrays & Function
• C Multi-dimensional Arrays

If you have a sound knowledge and understanding of what the functions of the concepts are then there will be no difficulty in understanding the given codes below. With all that said lets get coding!

Why Learn C Programming Language?

Because it mixes the characteristics of high-level languages with the functionalism of assembly language, C is often referred to as a middle-level computer language. The manipulation of bits, bytes, and addresses in C gives the programmer more control over how the program will behave and more direct access to the underlying hardware mechanisms.

Working programmers influenced, influenced, and field-tested C. As a result, C provides the programmer with exactly what he or she want. C++ is a more advanced version of the C programming language. C++ incorporates all of the features of C, as well as support for object-oriented programming (OOP). Furthermore, C++ includes numerous enhancements and features that make it a “better C,” regardless of whether or not it is used for object-oriented programming.

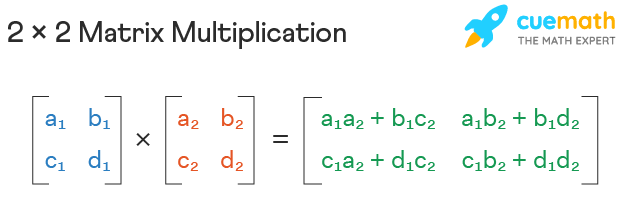
Multiplication of Matrices

Introduction

Matrix multiplication is a binary operation in mathematics that produces a matrix from two matrices, particularly in linear algebra. The number of columns in the first matrix must equal the number of rows in the second matrix for matrix multiplication to work. The resulting matrix, known as the matrix product, has the first matrix’s number of rows and the second matrix’s number of columns. AB stands for the product of matrices A and B.

Compatibility and Rules

If the number of columns in A equals the number of rows in B, two matrices A and B are said to be compatible. That instance, we can state that matrices A and B are compatible. If A is a matrix of order mn and B is a matrix of order np.

As we can see from above, two matrices can only be multiplied if they are compatible, which implies that the number of columns in the first matrix must equal the number of rows in the second matrix, in this case ‘n’.  If A is a matrix of order m×n and B is a matrix of order n×p, then the order of the product matrix is m×p. For example,

1) Multiplying a 4 x 3 matrix by a 3 x 4 matrix is compatible, and it produces a 4 x 4 matrix.

2) The 3 x 1 and 1 x 2 matrices are compatible, the product yields a 3 x 2 matrix.

3) It is not possible to multiply a 4 x 3 matrix by a 2 x 3 matrix.

Matrix Multiplication in C

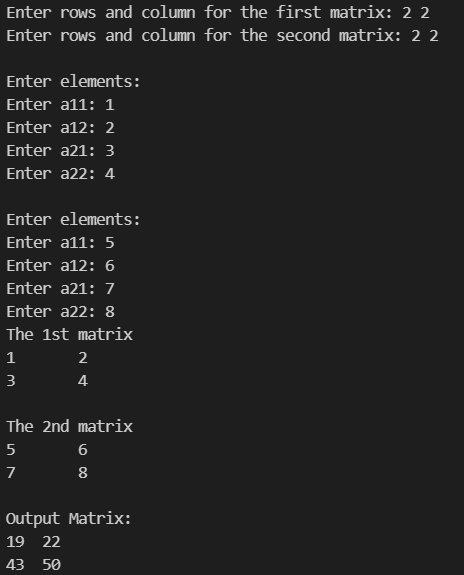
The best way to learn is to do. Hence, what better way to learn C programming language (if you know the basics) than to code your first mini project. In this tutorial we are going to multiply two user input matrices in c programming language. Keep in mind this is a mini project for absolute beginners and intermediate programmers as well.

// includnig the header files 
#include <stdio.h>
#include <stdlib.h>
#include <conio.h>

// function to get matrix elements entered by the user
void getMatrixElements(int matrix[][100], int row, int column) {

   printf("\nEnter elements: \n");

   for (int i = 0; i < row; ++i) {
      for (int j = 0; j < column; ++j) {
         printf("Enter a%d%d: ", i + 1, j + 1);
         scanf("%d", &matrix[i][j]);
      }
   }
}

// function to multiply two matrices
void multiplyMatrices(int first[][100],
                      int second[][100],
                      int result[][100],
                      int r1, int c1, int r2, int c2) {

   // Initializing elements of matrix mult to 0.
   for (int i = 0; i < r1; ++i) {
      for (int j = 0; j < c2; ++j) {
         result[i][j] = 0;
      }
   }

   // Multiplying first and second matrices and storing it in result
   for (int i = 0; i < r1; ++i) {
      for (int j = 0; j < c2; ++j) {
         for (int k = 0; k < c1; ++k) {
            result[i][j] += first[i][k] * second[k][j];
         }
      }
   }
}

// function to display the matrix
void display(int first[][100], int second[][100],int result[][100], int row, int column) {
    
    // displaying the first matrix 

    printf("The 1st matrix\n");
    for(int i=0;i<row;i++)
    {
        for(int j=0;j<column;j++)
        {
            printf("%d\t",first[i][j]);
        }
        printf("\n");
    }

    // displaying the second matrix 

    printf("\nThe 2nd matrix\n");
    for(int i=0;i<row;i++)
    {
        for(int j=0;j<column;j++)
        {
            printf("%d\t",second[i][j]);
        }
        printf("\n");
    }

    // displaying the ouput of the multiplication of the above two matrix 

   printf("\nOutput Matrix:\n");
   for (int i = 0; i < row; ++i) {
      for (int j = 0; j < column; ++j) {
         printf("%d  ", result[i][j]);
         if (j == column - 1)
            printf("\n");
      }
   }
}

int main() {
   int first[100][100], second[100][100], result[100][100], r1, c1, r2, c2;
   printf("Enter rows and column for the first matrix: ");
   scanf("%d %d", &r1, &c1);
   printf("Enter rows and column for the second matrix: ");
   scanf("%d %d", &r2, &c2);

   // Taking input until
   // 1st matrix columns is not equal to 2nd matrix row
   while (c1 != r2) {
      printf("Error! Enter rows and columns again.\n");
      printf("Enter rows and columns for the first matrix: ");
      scanf("%d%d", &r1, &c1);
      printf("Enter rows and columns for the second matrix: ");
      scanf("%d%d", &r2, &c2);
   }

   // get elements of the first matrix
   getMatrixElements(first, r1, c1);

   // get elements of the second matrix
   getMatrixElements(second, r2, c2);

   // multiply two matrices.
   multiplyMatrices(first, second, result, r1, c1, r2, c2);

   // display the result
   display(first, second, result, r1, c2);

   return 0;
}

Output