Basic Euclidean vector operations in C++

Euclidean vectors are very important quantity in mathematics, applied mathematics, physics, engineering etc. Formally vectors are those quantities which have both magnitude and direction. For example velocity. Velocity has both magnitude (Speed, like 2 Km/Hr) and direction (e.g. east). In the programmer’s perspective, there are many situation where you need to compute different vector operations. For example, consider a moving ball. To simulate the motion of ball, you must calculate the velocity of the ball. The ball has both magnitude (i.e rate of translation of position of center of the ball) and direction (e.g. axis x or y or z). This is just one example but there are various examples where vector operations are essential.
Now in this article, I will show you how to compute different vector operations like sum of two vectors, multiplication by scalar, dot product, cross product, normalization etc in C++. I choose C++ instead of C because it is object oriented. The vector can be represented by an object. The components of vector along x, y and z-axis will be the data member of the object. The data members are attributes of the object. Similarly, different operations will be the member functions of the object. Now the vector object can completely represent the vector quantity.

In this program, I have implemented as many vector operations as I can. For example summation of two vectors, difference of two vectors, magnitude, normalization of a vector, dot product and cross product of two vectors, multiplication and division by scalar quantity etc. Since vector is a user-defined data type (class) , treating them as a standard data type and trying to use built-in operations like +, –,*, / will result in error. For this, I have implemented operator overloading feature of C++. In this program, you will notice following operator overloaded

1. index []
2. Addition +
3. Subtraction  –
4. Multiplication *
5. Division –
6. Extraction <<
7. +=, –=, *=, /=
8. Unary – and +

Source Code:

#include <iostream>
#include <cmath>
using std::ostream;
using std::cout;
using std::cin;
using std::endl; 
class Vec3f {
    public:
        float v[3];
    public:
        Vec3f();
        Vec3f(float x, float y, float z); 
        float &operator[](int index);
        float operator[](int index) const; 
        Vec3f operator*(float scale) const;
        Vec3f operator/(float scale) const;
        Vec3f operator+(const Vec3f &other) const;
        Vec3f operator-(const Vec3f &other) const;
        Vec3f operator-() const; 
        const Vec3f &operator*=(float scale);
        const Vec3f &operator/=(float scale);
        const Vec3f &operator+=(const Vec3f &other);
        const Vec3f &operator-=(const Vec3f &other); 
        float magnitude() const;
        float magnitudeSquared() const;
        Vec3f normalize() const;
        float dot(const Vec3f &other) const;
        Vec3f cross(const Vec3f &other) const;
};
Vec3f::Vec3f() {
    v[0] = 0;
    v[1] = 0;
    v[2] = 0; 
} 
Vec3f::Vec3f(float x, float y, float z) {
    v[0] = x;
    v[1] = y;
    v[2] = z;
} 
float &Vec3f::operator[](int index) {
    return v[index];
} 
float Vec3f::operator[](int index) const {
    return v[index];
} 
Vec3f Vec3f::operator*(float scale) const {
    return Vec3f(v[0] * scale, v[1] * scale, v[2] * scale);
} 
Vec3f Vec3f::operator/(float scale) const {
    return Vec3f(v[0] / scale, v[1] / scale, v[2] / scale);
} 
Vec3f Vec3f::operator+(const Vec3f &other)  const{
    return Vec3f(v[0] + other.v[0], v[1] + other.v[1], v[2] + other.v[2]);
} 
Vec3f Vec3f::operator-(const Vec3f &other) const {
    return Vec3f(v[0] - other.v[0], v[1] - other.v[1], v[2] - other.v[2]);
} 
Vec3f Vec3f::operator-() const {
    return Vec3f(-v[0], -v[1], -v[2]);
} 
const Vec3f &Vec3f::operator*=(float scale) {
    v[0] *= scale;
    v[1] *= scale;
    v[2] *= scale;
    return *this;
} 
const Vec3f &Vec3f::operator/=(float scale) {
    v[0] /= scale;
    v[1] /= scale;
    v[2] /= scale;
    return *this;
} 
const Vec3f &Vec3f::operator+=(const Vec3f &other) {
    v[0] += other.v[0];
    v[1] += other.v[1];
    v[2] += other.v[2];
    return *this;
} 
const Vec3f &Vec3f::operator-=(const Vec3f &other) {
    v[0] -= other.v[0];
    v[1] -= other.v[1];
    v[2] -= other.v[2];
    return *this;
} 
float Vec3f::magnitude() const {
    return sqrt(v[0] * v[0] + v[1] * v[1] + v[2] * v[2]);
} 
float Vec3f::magnitudeSquared() const {
    return v[0] * v[0] + v[1] * v[1] + v[2] * v[2];
} 
Vec3f Vec3f::normalize() const {
    float m = sqrt(v[0] * v[0] + v[1] * v[1] + v[2] * v[2]);
    return Vec3f(v[0] / m, v[1] / m, v[2] / m);
} 
float Vec3f::dot(const Vec3f &other) const {
    return v[0] * other.v[0] + v[1] * other.v[1] + v[2] * other.v[2];
} 
Vec3f Vec3f::cross(const Vec3f &other) const {
    return Vec3f(v[1] * other.v[2] - v[2] * other.v[1],
                 v[2] * other.v[0] - v[0] * other.v[2],
                 v[0] * other.v[1] - v[1] * other.v[0]);
} 
ostream &operator<<(ostream &output, const Vec3f &v) {
    cout << '(' << v[0] << ", " << v[1] << ", " << v[2] << ')';
    return output;
} 
int main()
{
    Vec3f v1(2,3,-1);
    Vec3f v2(2,5,6);
    cout<<"v1 = "<<v1<<endl;
    cout<<"v2 = "<<v2<<endl;
    cout<<"v1 * 2 = "<<v1*2<<" and v1 / 2 = "<<v1/2<<endl;
    cout<<"v1 + v2 = "<<v1+v2<<endl;
    cout<<"v1 - v2 = "<<v1-v2<<endl;
    cout<<"-v1 = "<<-v1<<endl;
    cout<<"|v1| = "<<v1.magnitude()<<endl;
    cout<<"Normalized v1 = "<<v1.normalize()<<endl;
    cout<<"v1.v2 = "<<v1.dot(v2)<<endl;
    cout<<"v1xv2 = "<<v1.cross(v2)<<endl; 
}

Sample Output

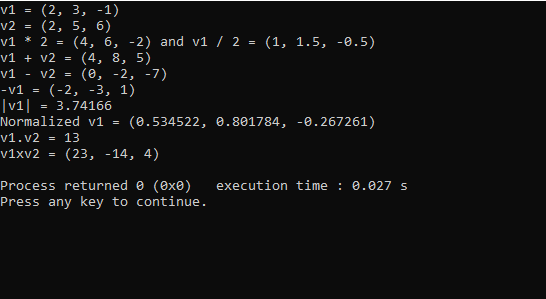
Same technique can be implemented to computer other quantities like Complex numbers, Matrix etc.

If you have any queries, please ask in the form of comment.