3D Rotation Algorithm about arbitrary axis with C/C++ code

1. Translate the object so that the rotation axis passes through the coordinate origin.
2. Rotate the object so that the axis of rotation coincides with one of the coordinate axes.
3. Perform the specified rotation about that coordinate axis.
4. Apply inverse rotations to bring the rotation axis back to its original orientation.
5. Apply the inverse translation to bring the rotation axis back to its original position.
   

Let (u, v, w) be a vector that specifies the axis about which the object is to be rotated. Suppose the vector passes through a point (a, b, c). Then the general composite matrix for the rotation can be written as:

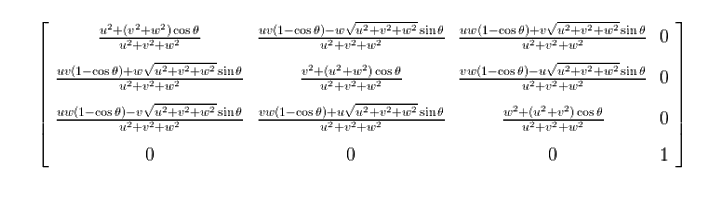
Here L is the magnitude of the axis vector. C source code for the arbitrary rotation is given below. Here (a, b, c) is assumed to be the origin for simplicity.

Source Code

#include <iostream>
#include <cmath> 
 
using namespace std; 
 
typedef struct {
    float x;
    float y;
    float z;
}Point;
Point points; 
 
float rotationMatrix[4][4];
float inputMatrix[4][1] = {0.0, 0.0, 0.0, 0.0};
float outputMatrix[4][1] = {0.0, 0.0, 0.0, 0.0}; 
 
void showPoint(){
    cout<<"("<<outputMatrix[0][0]<<","<<outputMatrix[1][0]<<","<<outputMatrix[2][0]<<")"<<endl;
} 
 
void multiplyMatrix()
{
    for(int i = 0; i < 4; i++ ){
        for(int j = 0; j < 1; j++){
            outputMatrix[i][j] = 0;
            for(int k = 0; k < 4; k++){
                outputMatrix[i][j] += rotationMatrix[i][k] * inputMatrix[k][j];
            }
        }
    }
}
void setUpRotationMatrix(float angle, float u, float v, float w)
{
    float L = (u*u + v * v + w * w);
    angle = angle * M_PI / 180.0; //converting to radian value
    float u2 = u * u;
    float v2 = v * v;
    float w2 = w * w; 
 
    rotationMatrix[0][0] = (u2 + (v2 + w2) * cos(angle)) / L;
    rotationMatrix[0][1] = (u * v * (1 - cos(angle)) - w * sqrt(L) * sin(angle)) / L;
    rotationMatrix[0][2] = (u * w * (1 - cos(angle)) + v * sqrt(L) * sin(angle)) / L;
    rotationMatrix[0][3] = 0.0; 
 
    rotationMatrix[1][0] = (u * v * (1 - cos(angle)) + w * sqrt(L) * sin(angle)) / L;
    rotationMatrix[1][1] = (v2 + (u2 + w2) * cos(angle)) / L;
    rotationMatrix[1][2] = (v * w * (1 - cos(angle)) - u * sqrt(L) * sin(angle)) / L;
    rotationMatrix[1][3] = 0.0; 
 
    rotationMatrix[2][0] = (u * w * (1 - cos(angle)) - v * sqrt(L) * sin(angle)) / L;
    rotationMatrix[2][1] = (v * w * (1 - cos(angle)) + u * sqrt(L) * sin(angle)) / L;
    rotationMatrix[2][2] = (w2 + (u2 + v2) * cos(angle)) / L;
    rotationMatrix[2][3] = 0.0; 
 
    rotationMatrix[3][0] = 0.0;
    rotationMatrix[3][1] = 0.0;
    rotationMatrix[3][2] = 0.0;
    rotationMatrix[3][3] = 1.0;
} 
 
int main()
{
    float angle;
    float u, v, w;
    cout<<"Enter the initial point you want to transform:";
    cin>>points.x>>points.y>>points.z;
    inputMatrix[0][0] = points.x;
    inputMatrix[1][0] = points.y;
    inputMatrix[2][0] = points.z;
    inputMatrix[3][0] = 1.0; 
 
    cout<<"Enter axis vector: ";
    cin>>u>>v>>w; 
 
    cout<<"Enter the rotating angle in degree: ";
    cin>>angle; 
 
    setUpRotationMatrix(angle, u, v, w);
    multiplyMatrix();
    showPoint(); 
 
    return 0;
}