Gaussian Filter generation using C/C++
Gaussian filtering is extensively used in Image Processing to reduce the noise of an image. In this article I will generate the 2D Gaussian Kernel that follows the Gaussian Distribution which is given
Where σ is the standard deviation of distribution, x is the distance from the origin in the horizontal axis, y is the distance from the origin in the vertical axis. The mean is assumed to be at origin O(0,0). The pictorial view of Gaussian Distribution for σ= 0 and mean at origin is
Source Code in C/C++
#include <iostream>
#include <cmath>
#include <iomanip>
using namespace std;
void createFilter(double gKernel[][5])
{
// set standard deviation to 1.0
double sigma = 1.0;
double r, s = 2.0 * sigma * sigma;
// sum is for normalization
double sum = 0.0;
// generate 5x5 kernel
for (int x = -2; x <= 2; x++)
{
for(int y = -2; y <= 2; y++)
{
r = sqrt(x*x + y*y);
gKernel[x + 2][y + 2] = (exp(-(r*r)/s))/(M_PI * s);
sum += gKernel[x + 2][y + 2];
}
}
// normalize the Kernel
for(int i = 0; i < 5; ++i)
for(int j = 0; j < 5; ++j)
gKernel[i][j] /= sum;
}
int main()
{
double gKernel[5][5];
createFilter(gKernel);
for(int i = 0; i < 5; ++i)
{
for (int j = 0; j < 5; ++j)
cout<<gKernel[i][j]<<"\t";
cout<<endl;
}
}
Output 5×5 Gaussian Kernel
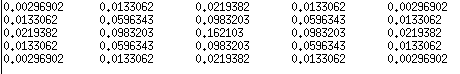
References:
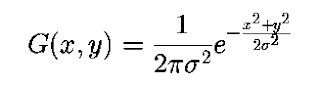




Thanks for your Blog entry, nice Example.
cool, thanks for sharing.
Look carefully i have write r*r in the formula. This answer was verified using MATLAB's Gaussian function
This comment has been removed by the author.
This comment has been removed by the author.
Hi!
What is the reason to sqrt and then do r*r? Why not just skip the sqrt and only use r?
Thanks a lot!
hi
i need source code in c++ to apply gaussian filter to gray image
i need code in c++ for apply gaussian filter to gray image