Calculating a convolution of an Image with C++: Image Processing

In convolution, the calculation performed at a pixel is a weighted sum of grey  levels from a neighbourhood surrounding a pixel. Grey levels taken from the neighbourhood are weighted by coefficients that come from a matrix or convolution kernel. The kernel’s dimensions define the size of the neighbourhood in which calculation take place. The most common dimension is 3×3. I am using this size of matrix in this article. During convolution, we take each kernel coefficient in turn and multiply it by a value from the neighbourhood of the image lying under the kernel. We apply the kernel to the image in such a way that the value at the top-left corner of the kernel is multiplied by the value at bottom-right corner of the neighbourhood. This can be expressed by following mathematical expression for kernel of size mxn.

Where h denotes the convolution kernel, f is the input pixel, g is the output pixel. Here n2 = n/2 and m2 = m/2. For 3×3 dimension of kernel, the above expression reduces to

Lets see an example. Suppose we have convolution matrix

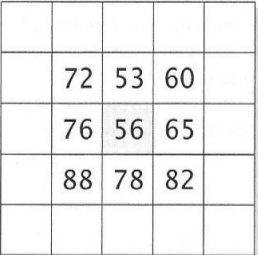
and part of the image pixel is

Now applying above expression, the value of a central pixel becomes

g(x, y) = -1 x 82 + 0 x 78 + 1 x 88 + -1 x 65 + 0 x 56 + 1 x 76 + -1 x 60 + 0 x 53 + 1 x 72 = 29

Algorithm for single pixel convolution can be written as ( for 3×3)

Create a Kernel of size 3×3 and fill the kernel with coefficients
sum = 0
for k = -1 to 1 do
   for j = -1 to 1 do
      sum = sum + h(j +1, k + 1)*f(x – j, y – k)
   end for
end for
g(x, y) = sum

The above discussion is mainly focused on single pixel operation. But the image doesn’t have only single pixel. To do the convolution operation on whole image, we must perform convolution on all pixels as follows

for y = 0 to image_height do
   for x = 0 to image_width do
      perform single pixel convolution
   end for
end for

But this algorithm has one limitation that it is impossible to calculate the convolution at borders. When we try to calculate convolution of pixel lying in image border, part of the kernel lies outside the image. To handle this limitation there are various approaches, some are given below

No processing at border

This is simple technique in which pixels at border are simply neglected. This can be done using following algorithm

for all pixel coordinates x and y, do
   g(x, y) = 0
end for
for y = 1 to image_height – 1
   for x = 1 to image_width – 1
      perform single pixel convolution
   end for
end for

Reflected Indexing

In this method, the pixel lying outside the image i.e. (x – j, y – k) are reflected back into the image by using following algorithm

if x < 0 then
   x = -x – 1
else if x >= image_width then
   x = 2*image_width – x – 1
end if

Circular Indexing

In this method, coordinates that exceed the bounds of the image wrap around to the opposite side using following algorithm

if x < 0 then
   x =  x + image_width
else if x >= image_width then

   x = x – image_width
end if

C++ implementation : Source Code

#include<iostream>
#include<opencv2/imgproc/imgproc.hpp>
#include<opencv2/highgui/highgui.hpp>
 
using namespace std;
using namespace cv;
 
int reflect(int M, int x)
{
    if(x < 0)
    {
        return -x - 1;
    }
    if(x >= M)
    {
        return 2*M - x - 1;
    }
   return x;
}
 
int circular(int M, int x)
{
    if (x<0)
        return x+M;
    if(x >= M)
        return x-M;
   return x;
}
 
 
void noBorderProcessing(Mat src, Mat dst, float Kernel[][3])
{
 
    float sum;
    for(int y = 1; y < src.rows - 1; y++){
        for(int x = 1; x < src.cols - 1; x++){
            sum = 0.0;
            for(int k = -1; k <= 1;k++){
                for(int j = -1; j <=1; j++){
                    sum = sum + Kernel[j+1][k+1]*src.at<uchar>(y - j, x - k);
                }
            }
            dst.at<uchar>(y,x) = sum;
        }
    }
}
 
void refletedIndexing(Mat src, Mat dst, float Kernel[][3])
{
    float sum, x1, y1;
    for(int y = 0; y < src.rows; y++){
        for(int x = 0; x < src.cols; x++){
            sum = 0.0;
            for(int k = -1;k <= 1; k++){
                for(int j = -1;j <= 1; j++ ){
                    x1 = reflect(src.cols, x - j);
                    y1 = reflect(src.rows, y - k);
                    sum = sum + Kernel[j+1][k+1]*src.at<uchar>(y1,x1);
                }
            }
            dst.at<uchar>(y,x) = sum;
        }
    }
}
 
void circularIndexing(Mat src, Mat dst, float Kernel[][3])
{
    float sum, x1, y1;
    for(int y = 0; y < src.rows; y++){
        for(int x = 0; x < src.cols; x++){
            sum = 0.0;
            for(int k = -1;k <= 1; k++){
                for(int j = -1;j <= 1; j++ ){
                    x1 = circular(src.cols, x - j);
                    y1 = circular(src.rows, y - k);
                    sum = sum + Kernel[j+1][k+1]*src.at<uchar>(y1,x1);
                }
            }
            dst.at<uchar>(y,x) = sum;
        }
    }
}
 
int main()
{
 
      Mat src, dst;
 
 
      /// Load an image
      src = imread("salt.jpg", CV_LOAD_IMAGE_GRAYSCALE);
 
      if( !src.data )
      { return -1; }
 
 
      float Kernel[3][3] = {
                            {1/9.0, 1/9.0, 1/9.0},
                            {1/9.0, 1/9.0, 1/9.0},
                            {1/9.0, 1/9.0, 1/9.0}
                           };
 
        dst = src.clone();
        for(int y = 0; y < src.rows; y++)
            for(int x = 0; x < src.cols; x++)
                dst.at<uchar>(y,x) = 0.0;
 
        circularIndexing(src, dst, Kernel);
 
 
 
        namedWindow("final");
        imshow("final", dst);
 
        namedWindow("initial");
        imshow("initial", src);
 
      waitKey();
 
 
    return 0;
}